यूपी एलटी ग्रेड गणित सिलेबस 2025 (UP LT Grade Maths Syllabus in Hindi PDF Download)
यूपी एलटी ग्रेड शिक्षक परीक्षा सिलेबस गणित (UP LT Grade Teacher Exam Syllabus Math in Hindi) - उत्तर प्रदेश लोक सेवा आयोग (यूपीपीएससी) द्वारा सहायक अध्यापक प्रशिक्षित स्नातक श्रेणी (पुरुष एवं महिला शाखा) परीक्षा 2025 के लिए जारी नोटिफिकेशन में परीक्षा की योजना और विषयवार सिलेबस जारी किया गया है। परीक्षा दो चरणों में आयोजित की जाएगी। इसमें पहले प्रारंभिक परीक्षा ली जाएगी। प्री परीक्षा में उत्तीर्ण अभ्यर्थी मुख्य परीक्षा में शामिल होंगे। यूपी एलटी ग्रेड शिक्षक भर्ती 2025 की योजना और गणित के विस्तृत सिलेबस को जानने के लिए पूरा लेख पढ़ें।
लेटेस्ट: उत्तर प्रदेश एलटी शिक्षक ग्रेड (यूपीपीएससी) की ओर से एलटी ग्रेड टीचर भर्ती 2025 के लिए एग्जाम डेट की घोषित कर दी गई है। कुल 6 विषयों के लिए परीक्षा 6, 7 एवं 21 दिसंबर 2025 को आयोजित की जाएगी। प्रत्येक दिन परीक्षा का आयोजन दो शिफ्ट में करवाया जायेगा। अन्य 9 विषयों के लिए एग्जाम शेड्यूल बाद में घोषित किया जायेगा।
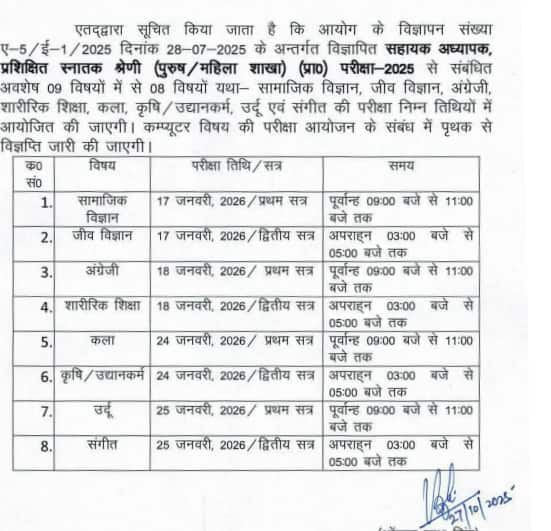
यूपी एलटी ग्रेड शिक्षक एग्जाम डेट की अधिसूचना देखें:
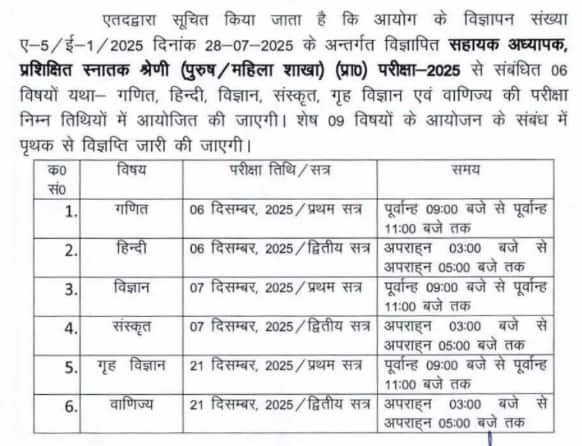
यूपी एलटी ग्रेड टीचर आवेदन पत्र के साथ ही आयोग ने एलटी ग्रेड शिक्षक भर्ती परीक्षा सिलेबस, परीक्षा पैटर्न, अंकन योजना और अन्य महत्वपूर्ण जानकारी भी एलटी ग्रेड शिक्षक भर्ती अधिसूचना में दी है।
यूपी एलटी ग्रेड शिक्षक भर्ती 2025 आवेदन पत्र
यूपी एलटी ग्रेड शिक्षक भर्ती 2025 - एक नजर (UP LT Grade Teacher Recruitment 2025 Dates-Overview in hindi)
मुख्य बिंदु | विवरण |
परीक्षा का नाम | उत्तर प्रदेश लाइसेंसधारी ग्रेड शिक्षक/ यूपी एलटी शिक्षक ग्रेड (Uttar Pradesh Licentiate Teacher Grade) |
रिक्तियों की संख्या | 7466 (पुरुष - 4860, महिला - 2525, बैकलॉग - 81) |
परीक्षा संचालक | उत्तर प्रदेश लोक सेवा आयोग |
आवेदन की तिथि | 28 जुलाई से 28 अगस्त 2025 |
आधिकारिक वेबसाइट | https://uppsc.up.nic.in/ |
ये भी पढ़ें -
सीटेट 2025 - आवेदन, परीक्षा तिथि
सीटेट 2025 आवेदन प्रक्रिया और तिथियां
सीटेट परीक्षा पैटर्न 2025
इसे भी देखें - रीट परीक्षा 2025
यूपी एलटी ग्रेड शिक्षक परीक्षा पैटर्न और सिलेबस
यूपी एलटी ग्रेड शिक्षक भर्ती परीक्षा के प्रथम चरण में प्रारंभिक परीक्षा में वस्तुनिष्ठ 150 प्रश्न पूछे जाएंगे। इस पेपर में सामान्य अध्ययन के 30 प्रश्न और प्रत्येक वैकल्पिक मुख्य विषय से 120 प्रश्न होंगे। प्रत्येक प्रश्न 2 अंक के होंगे यानी कुल 300 अंकों का पेपर होगा। प्रश्न पत्र हल करने के लिए 2 घंटे की समयावधि होगी। प्रथम चरण की परीक्षा पास करने वाले अभ्यर्थी द्वितीय चरण की मुख्य परीक्षा में शामिल हो सकेंगे। विस्तृत जानकारी के लिए लेख को विस्तार से पढ़ें।
यूपी एलटी ग्रेड शिक्षक भर्ती विस्तृत अधिसूचना देखें
ये भी पढ़ें :
यूपी एलटी ग्रेड शिक्षक भर्ती 2025 तिथियां (UP LT Grade Teacher Recruitment 2025 Dates)
मुख्य इवेंट्स | यूपी एलटी ग्रेड शिक्षक तारीखें |
यूपी एलटी ग्रेड शिक्षक भर्ती अधिसूचना | 28 जुलाई 2025 |
यूपी एलटी ग्रेड शिक्षक आवेदन 2025 | 28 जुलाई 2025 |
यूपी एलटी ग्रेड शिक्षक आवेदन अंतिम तिथि | 28 अगस्त 2025 |
यूपी एलटी शिक्षक ग्रेड आवेदन सुधार अंतिम तिथि | 4 सितंबर 2025 |
यूपी एलटी ग्रेड शिक्षक परीक्षा एडमिट कार्ड | सूचित किया जाएगा |
यूपी एलटी ग्रेड शिक्षक परीक्षा 2025 | 6, 7 और 21 दिसंबर 2025 |
यूपी एलटी ग्रेड शिक्षक परीक्षा परिणाम | सूचित किया जाएगा |
ये भी पढ़ें :
यूपी एलटी ग्रेड परीक्षा सिलेबस (UP LT teacher grade exam syllabus in hindi)
उत्तर प्रदेश स्नातक स्तर शिक्षक भर्ती परीक्षा का सिलेबस आधिकारिक अधिसूचना के साथ जारी किया गया है। यूपी एलटी ग्रेड शिक्षक सिलेबस (UP LT grade teacher syllabus in hindi) में पेपर 1 सामान्य अध्ययन के लिए और पेपर 2 मुख्य विषय के लिए है। इस लेख में नीचे गणित का विस्तृत सिलेबस प्रदान किया गया है।
ये भी पढ़ें :
प्रारम्भिक एवं मुख्य परीक्षा हेतु गणित का विस्तृत पाठ्यक्रम
संगत पाठ्यक्रम के आधार पर वैकल्पिक मुख्य विषयों के प्रश्नपत्रों की रचना हेतु प्रश्नपत्रों के स्वरूप एवं अंकों का विभाजन निम्नवत् है।-
1- मुख्य परीक्षा के सभी प्रश्न अनिवार्य होंगे तथा वे दो खण्डों में विभाजित रहेंगे। प्रश्नों की कुल संख्या
खण्डवार निम्नवत होंगेः-
खंड अ के अन्तर्गत 10 प्रश्न, लघु उत्तरीय (उत्तरों की शब्द सीमा 125) एवं प्रत्येक प्रश्न 08 अंक का होगा।
खंड ब के अन्तर्गत 10 प्रश्न, दीर्घ उत्तरीय (उत्तरों की शब्द सीमा 200) एवं प्रत्येक प्रश्न 12 अंक का होगा।
प्रारम्भिक एवं मुख्य परीक्षा हेतु विज्ञापन में विषयवार मुद्रित पाठ्यक्रम एक समान रहेगा।
सहायक अध्यापक, प्रशिक्षित स्नातक श्रेणी (पुरुष/महिला) तथा दिव्यांगजन सशक्तीकरण विभाग के अन्तर्गत सहायक अध्यापक पद हेतु विज्ञान पाठ्यक्रम
विषय-गणित
1-बीजगणित : समीकरण सिद्वान्त, समान्तर गुणोत्तर एवं हरात्मक श्रेणियाँ, प्राकृतिक संख्याओं के वर्गों एवं घनों का योग, क्रमचय एवं संचय, द्विपद प्रमेय, चरघातांकीय एवं लघुगणकीय श्रेणियाँ।
समुच्चय का बीजगणित संबंध एवं फलन, संबंधो के प्रकार, तुल्यता संबंध, फलनों के प्रकार, फलनों का संयोजन, प्रतिलोम फलन, समुच्चय पर द्विआधारी संक्रियायें, समूह, उपसमूह, प्रासामान्य समूह, आशिंक समूह, चकीय समूह, समूह के अवयव की कोटि, क्रमचय समूह, सम एवं विषम क्रमचय, लाग्रांज प्रमेय और इसके परिणाम, समूह समाकारिता।
सारणिक, आव्यूह के प्रकार, आव्यूहों पर बीजगणितीय संक्रियायें, सममित एवं विषम सममित आव्यूह, हर्मिटीय एवं विषम हर्मिटीय आव्यूह, आव्यूह का प्रतिलोम, आव्यूह की जाति, आव्यूह का रेखीय समीकरणों के निकाय को हल करने में अनुप्रयोग, आव्यूह के आईगेनमान एवं आईगेन सदिश, कैले हैमिल्टन प्रमेय और इसके अनुप्रयोग।
2- वास्तविक विश्लेषण : वास्तविक संख्याओं के अनुक्रम, परिबद्ध एवं एकदिष्ट अनुकम, अभिसारी अनुकम, धनात्मक पदों की श्रेणियों का अभिसरण, तुलनात्मक परीक्षण, काशी का nवां मूल परीक्षण, अनुपात परीक्षण, रबे परीक्षण, लघुगणकीय और द मार्गन एवं बर्टेण्ड परीक्षण, एकान्तर श्रेणी एवं लैबनिट्ज परीक्षण।
3- सदिश विश्लेषण : सदिशों पर संक्रियायें, दो और तीन सदिशों का अदिश एवं सदिश गुणन और उनके अनुप्रयोग, सदिश अवकलन, ग्रेडियन्ट, डाईवर्जेन्स एवं कर्ल।
4- सम्मिश्र विश्लेषण : सम्मिश्र संख्यायें, एक सम्मिश्र चर के फलन, द मायवर प्रमेय और इसके अनुप्रयोग, ईकाई के nवें मूल, एक सम्मिश्र फलन के चर घातांकी, सीधे एवं व्युत्कम त्रिकोणमितीय, हाईपरबोलिक एवं लघुगणकीय फलन, सम्मिश्र फलनों की सांत्यता एवं अवकलनीयता, काशी रीमान समीकरण, वैश्लेशिक फलन, प्रसंवादी फलन ।
5- कलन : फलन की सीमा, सांतत्यता एवं अवकलनीयता रोल का प्रमेय, लाग्रान्ज का मध्यमान प्रमेय, लापिताल नियम, उत्तरोत्तर अवकलन, स्पर्शी एवं अभिलम्ब, उच्चिष्ठ एवं निम्निष्ठ, वर्धमान व ह्रासमान फलन, दो चरों के फलन की सीमा, सांतत्यता एवं अवकलनीयता, आंशिक अवकलन समाकलन की विधियाँ, निश्चित समाकल, वक्रों द्वारा परिबद्ध क्षेत्रफल, वक्र की लम्बाई, घूर्णन द्वारा बने ठोसों का पृष्ठीय क्षेत्रफल एवं आयतन को ज्ञात करने में समाकलन का अनुप्रयोग। प्रथम कोटि एवं प्रथम घात के अवकलन समीकरणों का हल ।
6- ज्यामिति : द्वितीय घात के व्यापक समीकरण तथा इसका रेखायुग्म, वृत्त, परवलय, दीर्घवृत्त एवं अतिपरवलय के रूप मे वर्गीकरण, अतिपरवलय के अनन्तस्पर्शी, मूल बिन्दु का विस्थापन एवं निर्देशांक अक्षों का घूर्णन, रेखा की दिक्कोज्यायें एवं दिक्अनुपात, समतल का कार्तीय एवं सदिश समीकरण, रेखा का कार्तीय एवं सदिश समीकरण, समतलीय एवं असमतलीय रेखायें, दो रेखाओं के बीच की न्यूनतम दूरी, दो समतलों के बीच, दो रेखाओं के बीच, एक रेखा एवं एक समतल के बीच के कोण, एक बिन्दु की एक समतल से दूरी, गोला, शंकु एवं बेलन।
7- सांख्यिकी एवं प्रायिकता : बरंबारता बंटन, सांख्यिकीय आंकड़ों का आलेखीय निरूपण, केन्द्रीय प्रवृत्ति की मापें, सामूहिक तथा असामूहिक आंकड़ों के माध्य, माध्यिका एवं बहुलक, प्रायिकता के योग एवं गुणन की प्रमेय।
8. संख्या पद्धति, बीजगणित का आधारभूत प्रमेय, त्रिभुज संबंधी प्रमेय, द्विघात समीकरण, त्रिकोणमिति, निर्देशांक ज्यामिति एवं क्षेत्रमिति।
अन्य लेख:
